Graph Concepts
Factor graphs are bipartite consisting of variables and factors, which are connected by edges to form a graph structure. The terminology of nodes is reserved for actually storing the data on some graph oriented technology.
What are Variables and Factors
Variables, denoted as the larger nodes in the figur below, represent state variables of interest such as vehicle or landmark positions, sensor calibration parameters, and more. Variables are likely hidden values which are not directly observed, but we want to estimate them them from observed data and at least some minimal algebra structure from probabilistic measurement models.
Factors, the smaller nodes in the figure, represent the algebraic interaction between particular variables, which is captured through edges. Factors must adhere to the limits of probabilistic models – for example conditional likelihoods capture the likelihood correlations between variables; while priors (unary to one variable) represent absolute information to be introduced. A heterogeneous factor graph illustration is shown below; also see a broader discussion linked on the literature page.
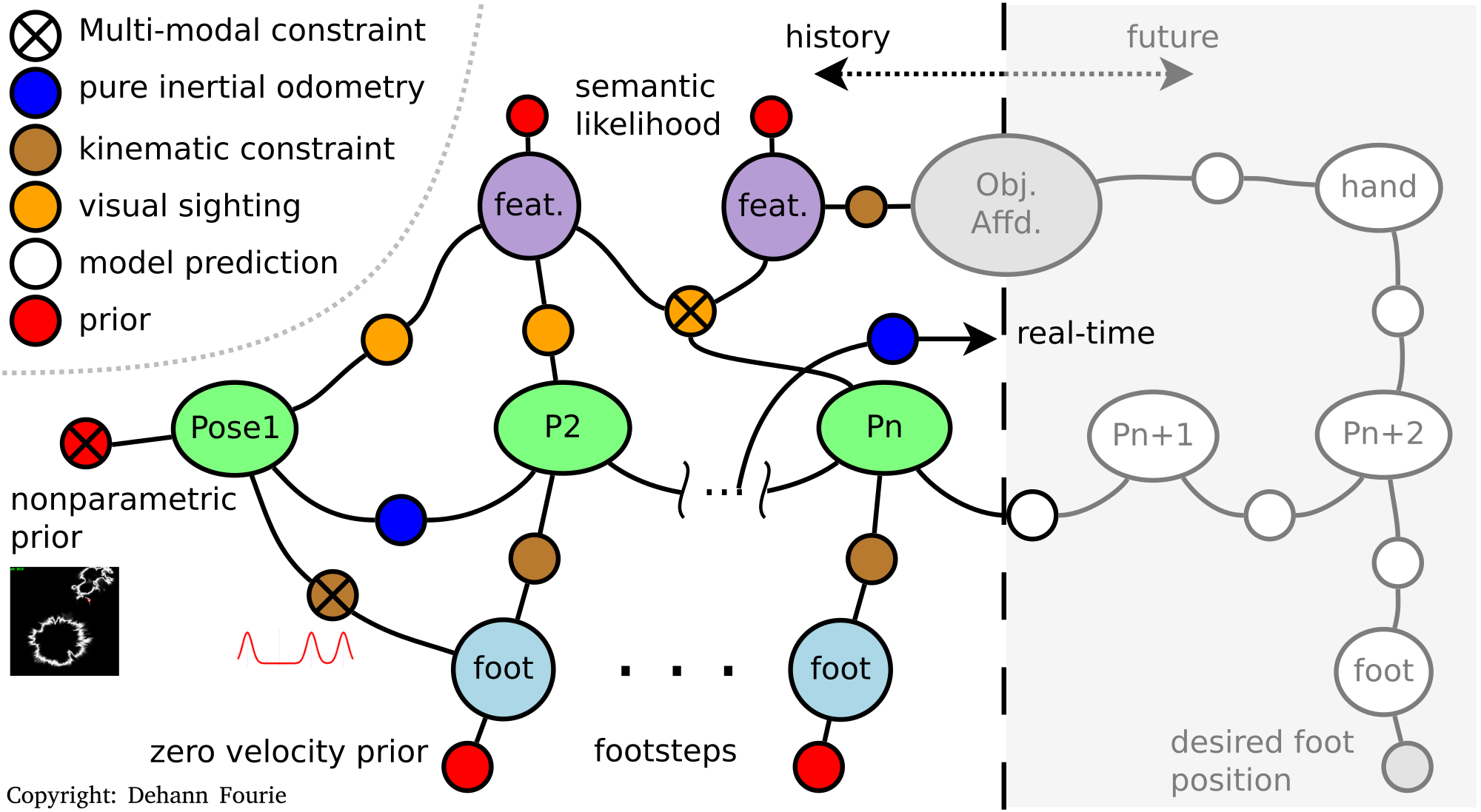
We assume factors are constructed from statistically independent measurements (i.e. no direct correlations between measurements other than the known algebraic model that might connect them), then we can use Probabilistic Chain rule to write inference operation down (unnormalized):
\[P(\Theta | Z) \propto P(Z | \Theta) P(\Theta)\]
This unnormalized "Bayes rule" is a consequence of two ideas, namely the probabilistic chain rule where Theta represents all variables and Z represents all measurements or data
\[P(\Theta , Z) = P(Z | \Theta) P(\Theta)\]
or similarly,
\[P(\Theta, Z) = P(\Theta | Z) P(Z).\]
The inference objective is to invert this system, so as to find the states given the product between all the likelihood models (based on the data):
\[P(\Theta | Z) \propto \prod_i P(Z_i | \Theta_i) \prod_j P(\Theta_j)\]
We use the uncorrelated measurement process assumption that measurements Z are independent given the constructed algebraic model.
Strictly speaking, factors are actually "observed variables" that are stochastically "fixed" and not free for estimation in the conventional SLAM perspective. Waving hands over the fact that factors encode both the algebraic model and the observed measurement values provides a perspective on learning structure of a problem, including more mundane operations such as sensor calibration or learning of channel transfer models.