Adding Velocity (Preintegration)

This tutorial describes how a new factor can be developed, beyond the pre-existing implementation in RoME.jl. Factors can accept any number of variable dependencies and allow for a wide class of allowable function calls can be used. Our intention is to make it as easy as possible for users to create their own factor types.

Example: Adding Velocity to RoME.Point2

A smaller example in two dimensions where we wish to estimate the velocity of some target: Consider two variables :x0 with a prior as well as a conditional–-likelihood for short–-to variable :x1. Priors are in the "global" reference frame (how ever you choose to define it), while likelihoods are in the "local" / "relative" frame that only exist between variables.

Brief on Variable Node softtypes

Variable nodes retain meta data (so called "soft types") describing the type of variable. Common VariableNode types are RoME.Point2D, RoME.Pose3D. VariableNode soft types are passed during construction of the factor graph, for example:

v1 = addVariable!(fg, :x1, Pose2)

Certain cases require that more information be retained for each VariableNode, and velocity calculations are a clear example where time stamp data across positions is required.

Note Larger data can also be stored under the bigdata framework which is discussed here (TBD).

If the required VariableNode does not exist, then one can be created, such as adding velocity states with DynPoint2:

mutable struct DynPoint2 <: IncrementalInference.InferenceVariable
  ut::Int64 # microsecond time
  dims::Int
  DynPoint2(;ut::Int64=0) = new(ut, 4)
end

The dims field is permanently set to 4, i.e. [x, y, dx/dt, dy/dt]. The utparameter is for storing the microsecond time stamp for that variable node.

In order to implement your own factor type outside IncrementalInference you should import the required identifiers, as follows:

using IncrementalInference
import IncrementalInference: getSample

Note that new factor types can be defined at any time, even after you have started to construct the FactorGraph object.

DynPoint2VelocityPrior

Work in progress.

mutable struct DynPoint2VelocityPrior{T} <: IncrementalInference.AbstractPrior where {T <: Distribution}
  z::T
  DynPoint2VelocityPrior{T}() where {T <: Distribution} = new{T}()
  DynPoint2VelocityPrior(z1::T) where {T <: Distribution} = new{T}(z1)
end
getSample(dp2v::DynPoint2VelocityPrior, N::Int=1) = (rand(dp2v.z,N), )

DynPoint2DynPoint2 (preintegration)

The basic idea is that change in position is composed of three components (originating from double integration of Newton's second law):

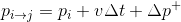( eq. 1)

DynPoint2DynPoint2 factor is using the above equation to define the difference in position between the two DynPoint2s. The position part stored in DynPoint2DynPoint2 factor corresponds to . A new multi-variable (so called "pairwise") factor between any number of variables is defined with three elements:

• Factor type definition that inherits either IncrementalInference.FunctorPairwise or IncrementalInference.FunctorPairwiseMinimize;

mutable struct DynPoint2DynPoint2{T} <: IncrementalInference.FunctorPairwise where {T <: Distribution}
  z::T
  DynPoint2DynPoint2{T}() where {T <: Distribution} = new{T}()
  DynPoint2DynPoint2(z1::T) where {T <: Distribution} = new{T}(z1)
end

• A sampling function with exactly the signature: getSample(dp2dp2::DynPoint2DynPoint2, N::Int=1) and returning a Tuple (legacy reasons);

getSample(dp2dp2::DynPoint2DynPoint2, N::Int=1) = (rand(dp2dp2.z,N), )

• A residual or minimization function with exactly the signature described below.

Residual (related to FunctorPairwise) or factor minimization function (related to FunctorPairwiseMinimize) signatures should match this dp2dp2::DynPoint2DynPoint2 example:

function (dp2dp2::DynPoint2DynPoint2)(
            res::Array{Float64},
            userdata,
            idx::Int,
            meas::Tuple,
            Xs...  )::Nothing

where Xs can be expanded to the particular number of variable nodes this factor will be associated, and note they are order sensitive at addFactor!(fg, ...) time. The res parameter is a vector of the same dimension defined by the largest of the Xs terms. The userdata value contains the small metadata / userdata portions of information that was introduced to the factor graph at construction time – please consult error(string(fieldnames(userdata))) for details at this time. This is a relatively new feature in the code and likely to be improved. The idx parameter represents a legacy index into the measurement meas[1] and variables Xs to select the desired marginal sample value. Future versions of the code plan to remove the idx parameter entirely. The Xs array of parameter are each of type ::Array{Float64,2} and contain the estimated samples from each of the current best marginal belief estimates of the factor graph variable node.

function (dp2dp2::DynPoint2DynPoint2)(
            res::Array{Float64},
            userdata,
            idx::Int,
            meas::Tuple,
            Xi::Array{Float64,2},
            Xj::Array{Float64,2}  )
  #
  z = meas[1][:,idx]
  xi, xj = Xi[:,idx], Xj[:,idx]
  dt = (userdata.variableuserdata[2].ut - userdata.variableuserdata[1].ut)*1e-6   # roughly the intended use of userdata
  res[1:2] = z[1:2] - (xj[1:2] - (xi[1:2]+dt*xi[3:4]))
  res[3:4] = z[3:4] - (xj[3:4] - xi[3:4])
  nothing
end

A brief usage example looks as follows, and further questions about how the preintegration strategy was implemented can be traced through the original issue JuliaRobotics/RoME.jl#60 or the literature associated with this project, or contact for more information.

using RoME, Distributions
fg = initfg()
v0 = addVariable!(fg, :x0, DynPoint2(ut=0))

# Prior factor as boundary condition
pp0 = DynPoint2VelocityPrior(MvNormal([zeros(2);10*ones(2)], 0.1*eye(4)))
f0 = addFactor!(fg, [:x0;], pp0)

# conditional likelihood between Dynamic Point2
v1 = addVariable!(fg, :x1, DynPoint2(ut=1000_000)) # time in microseconds
dp2dp2 = DynPoint2DynPoint2(MvNormal([10*ones(2);zeros(2)], 0.1*eye(4)))
f1 = addFactor!(fg, [:x0;:x1], dp2dp2)

initAll!(fg)
tree = wipeBuildNewTree!(fg)
inferOverTree!(fg, tree)

using KernelDensityEstimate
@show x0 = getKDEMax(getBelief(fg, :x0))
# julia> ... = [-0.19441, 0.0187019, 10.0082, 10.0901]
@show x1 = getKDEMax(getBelief(fg, :x1))
 # julia> ... = [19.9072, 19.9765, 10.0418, 10.0797]

VelPoint2VelPoint2 (back-differentiation)

In case the preintegrated approach is not the first choice, we include VelPoint2VelPoint2 <: IncrementalInference.FunctorPairwiseMinimize as a second likelihood factor example which may seem more intuitive:

mutable struct VelPoint2VelPoint2{T} <: IncrementalInference.FunctorPairwiseMinimize where {T <: Distribution}
  z::T
  VelPoint2VelPoint2{T}() where {T <: Distribution} = new{T}()
  VelPoint2VelPoint2(z1::T) where {T <: Distribution} = new{T}(z1)
end
getSample(vp2vp2::VelPoint2VelPoint2, N::Int=1) = (rand(vp2vp2.z,N), )
function (vp2vp2::VelPoint2VelPoint2)(
                res::Array{Float64},
                userdata,
                idx::Int,
                meas::Tuple,
                Xi::Array{Float64,2},
                Xj::Array{Float64,2}  )
  #
  z = meas[1][:,idx]
  xi, xj = Xi[:,idx], Xj[:,idx]
  dt = (userdata.variableuserdata[2].ut - userdata.variableuserdata[1].ut)*1e-6   # roughly the intended use of userdata
  dp = (xj[1:2]-xi[1:2])
  dv = (xj[3:4]-xi[3:4])
  res[1] = 0.0
  res[1] += sum((z[1:2] - dp).^2)
  res[1] += sum((z[3:4] - dv).^2)
  res[1] += sum((dp/dt - xi[3:4]).^2)  # (dp/dt - 0.5*(xj[3:4]+xi[3:4])) # midpoint integration
  res[1]
end

A similar usage example here shows:

fg = initfg()

# add three point locations
v0 = addVariable!(fg, :x0, DynPoint2(ut=0))
v1 = addVariable!(fg, :x1, DynPoint2(ut=1000_000))
v2 = addVariable!(fg, :x2, DynPoint2(ut=2000_000))

# Prior factor as boundary condition
pp0 = DynPoint2VelocityPrior(MvNormal([zeros(2);10*ones(2)], 0.1*eye(4)))
f0 = addFactor!(fg, [:x0;], pp0)

# conditional likelihood between Dynamic Point2
dp2dp2 = VelPoint2VelPoint2(MvNormal([10*ones(2);zeros(2)], 0.1*eye(4)))
f1 = addFactor!(fg, [:x0;:x1], dp2dp2)

# conditional likelihood between Dynamic Point2
dp2dp2 = VelPoint2VelPoint2(MvNormal([10*ones(2);zeros(2)], 0.1*eye(4)))
f2 = addFactor!(fg, [:x1;:x2], dp2dp2)

# Graphs.plot(fg.g)
initAll!(fg)
tree = wipeBuildNewTree!(fg)
inferOverTree!(fg, tree)

# see the output
@show x0 = getKDEMax(getBelief(getVariable(fg, :x0)))
@show x1 = getKDEMax(getBelief(getVariable(fg, :x1)))
@show x2 = getKDEMax(getBelief(getVariable(fg, :x2)))

Producing output:

x0 = getKDEMax(getBelief(getVariable(fg, :x0))) = [0.101503, -0.0273216, 9.86718, 9.91146]
x1 = getKDEMax(getBelief(getVariable(fg, :x1))) = [10.0087, 9.95139, 10.0622, 10.0195]
x2 = getKDEMax(getBelief(getVariable(fg, :x2))) = [19.9381, 19.9791, 10.0056, 9.92442]

IncrementalInference.jl Defining Factors (Future API)

We would like to remove the idx indexing from the residual function calls, since that is an unnecessary burden on the user. Instead, the package will use views and SubArray types to simplify the interface. Please contact author for more details (8 June 2018).

Contributions

Thanks to mc2922 for raising the catalyst issue and conversations that followed from JuliaRobotics/RoME.jl#60.